エクセルで複利計算をする方法

Excel / By / February 10, 2023

アルバート・アインシュタインはかつて、「複利は世界の八番目の不思議である」と言った。それを理解する者はそれを獲得し、理解しない者はそれを支払うのだ"。

複利は世界で最も強力な金融概念の一つかもしれませんが、計算するのはそれほど難しくなく、Excelを使えばさらに簡単に計算することができます。複利とは、金融の概念で、ローンや預金の利息を、当初の元本と過去の期間の累積利息の両方に基づいて計算することを指します。

複利の普通預金口座にお金を入れておくと、利息がつくたびに、その利息が口座の残高に加算されていきます。そのため、次に利息が計算されるときは、より高い残高に基づいて計算され、より多くの利息を得ることができます。時間が経つにつれて、単利と比較してはるかに速い成長につながります。複利は、普通預金、譲渡性預金、債券など、さまざまな金融商品で利用されています。

このチュートリアルでは、単利複利、逆利複利、連続複利の計算方法をExcelの例を使って説明します。また、異なる複利回数に対応した複利のテンプレートや電卓の作成方法もご紹介します。

単利と複利の比較

単利と複利は、ローンや投資の利息を計算する2つの異なる方法です。この2つの主な違いは、利息の計算方法と、時間の経過とともに元金に加算される方法です。

単利です。単利は、元本金額と金利のみに基づいて計算されます。単利は複利ではないので、各期に得られる利息は元本に加算されず、従って複利のように残高が急速に増えることはない。

複利。複利は、元本と前期の累積利息の両方に基づいて計算されます。複利では、各期間に獲得した利息が元本に加算されるため、時間の経過とともに残高が急速に増加する。

結論から言うと、複利は単利に比べて、稼いだ利子を再投資するため、富や負債をより早く成長させることができます。

エクセルで演算子を使った複利の計算

Excel で複利を計算する方法を簡単な算術式で見て、複利がどのように機能するかを理解しましょう。次のセクションでは、異なる複利計算期間での投資の将来価値を計算することになりますが、まず、複利計算で投資が年、月、四半期などにどのように増加するかを見ていきます。

算術式による年利の複利

100ドルを年利5％で投資しているとして、その投資が複利でどのように成長していくかを知りたい場合、次のような公式が使えます。

=元本金額 * (1利息)

この例では、計算式は

==B1*(1 $D$1)

ここで、B1 は初期投資額 (すなわち 100 ドル)、$D$1 は利息 (すなわち 5%)です。ご覧のように、セルD1への参照を$記号で固定しているのは、利息は毎年変わらないので、次のステップで数式をコピーしても変更されないからです。

Excelはパーセンテージを10進数で表示するため、0%から100までのパーセンテージは0から1までの10進数で表示されるのと同じです。例えば、1%は100の1乗、つまり0.01ですから、5%は0.05ということになります。ここで、利息は1年に1回複利で支払われるので、(1 $D$1) または (1 0.05) となります。つまり、1年後の投資額は105ドルになります。

さて、2年後の残高を計算する必要があります。そのためには、「1年目の終わり」の残高、つまり105ドルを使って、同じ利率で複利計算をすることになります。これは、同じ数式をセルB3、B4、B5などにコピーして行うことができます。塗りつぶしハンドルをドラッグして、数式をコピーします。

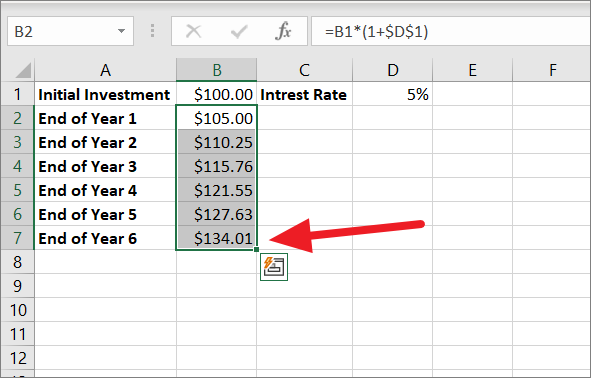
6年目の終わりには、招待額が134.01ドルに増額されます。

これも、最初の金額である100ドルに、1年ごとに1.05をかけることで計算することができます。そして、その値を小数点以下2桁に切り上げれば、同じ結果になります。

6年後の残高を求めるには、100ドルに1.05を6回かければよい。

=100*1.05*1.05*1.05*1.05*1.05*1.05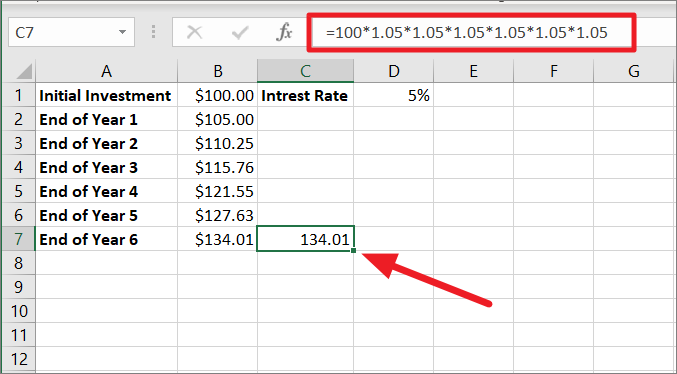

複利の計算式

複利計算の構文は以下の通りです。

複利計算＝最終金額-初期金額

複利計算で得た利息の総額を計算したい場合は、最終金額または将来価値（B7）から初期金額（B1）または開始金額を差し引くだけです。

=B7-B1 =134.01-100 =34.01

6年間蓄積された複利は34.01である。

上記の計算式は、Excelで単純な複利計算がどのように機能するかを示しています。しかし、投資の将来価値を計算するとなると、これらの計算式では不十分です。また、日次、週次、月次、四半期、半期と異なる複利計算期間での将来価値（最終的な価値）を計算することは、これらの公式ではできません。

異なる複利計算期間のための数学的複利計算式

年複利、四半期複利、月複利、週複利、日複利でいくら稼げるかを計算するのに使える簡単な数式がもうひとつあります。幸いなことに、この数式では表全体を作成する必要はなく、期間と金利を指定して将来の価値を計算するだけでよいのです。

複利で最終的な金額や将来価値を計算するには、当初の元本金額、利率、複利回数、年数が必要です。

構文です。

構文は以下の通りです。

fv = pv * (1 r/n)^t*n

ここで

  • FV – 複利を適用した後の投資の将来価値または最終的な価値を指します。
  • PV – 現在価値とは、投資した当初の金額または元本を指します。パーセンテージを指定する場合、％、10進数、分数を使用することができます。例えば、10は0.1または10/100と指定することができます。
  • R – 年利率です。
  • N – 1年間に複利計算が行われる回数 (例: 1年間、4四半期、12ヶ月間など)。
  • T – 複利が適用される年数．

さて、上記の複利計算式を使って、異なる複利計算頻度で投資の最終価値または将来価値を計算することができます。

  • 年複利計算。
  • 四半期ごとの複利計算
  • 月次および週次複利計算。
  • 日次複利計算

数式を使った年複利計算

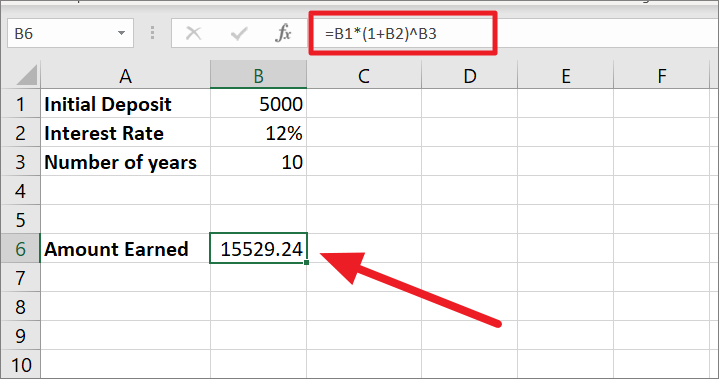
あなたが普通預金口座に5000円入金し、銀行が年複利で10％の金利を提供しているとします。さて、10年後のリターンはいくらか知りたいですよね。これは、年複利計算で使う式です。

=B1*(1 B2)^B3

または

=b1*(1 b2/1)^b3*1=5000 * (1 12%/1)^10*1=5000 * (112%)^10=5000 * 3.105848=15529.24

年複利なので、1年に1回だけ複利計算される。そこで、金利10%を1で割って1に加え、1 12quals 112%（1が100%なので、1 12% = 112%）となる。

その後、キャレット記号(^)で数値を上げたり、指数を与えたりする。112%は年数として10の累乗（10*1）になり、3.105848%になる。最後に、5000に3.105848を掛けて、将来の価値である15529.24を得ます。これが、最初の預金5000を12%の金利で10年間運用した場合の最終的な獲得金額です。

この計算式は、銀行や金融機関が複利の計算に用いるものと類似しています。

初回預入時に得られる利息を求めるには、最終金額から初回金額を引きます。

複利＝将来価値-初期価値

複利＝15529.24-5000円

複利＝10529.24

数式でわかる半年複利計算

では、半年複利の計算方法を説明します。半年複利は、半年ごとに複利計算を行いますので、1年に2回複利計算を行うことになります。

半年ごとの複利計算を行うには、同じ計算式のN値（複利計算を行う回数）を変更するだけです。

=b1*(1 b2/2)^(b3*2)

また、Nの値を直接指定するのではなく、引数の値の入っているセルを参照することで、このような数式を書くこともできる。

=b1*(1 b2/2)^(b3*2)

ここでは年2回の複利計算なので、12％の金利を2で割ると0.06となります。0.06に1を足すと1.06となります。年数(10)に複利計算の回数(2)をかけて、その結果(20)を指数とする。

1.06を20乗すると、3.207135472となります。最後に、3.207135472に元本残高5000を掛けると、16035.68となります。

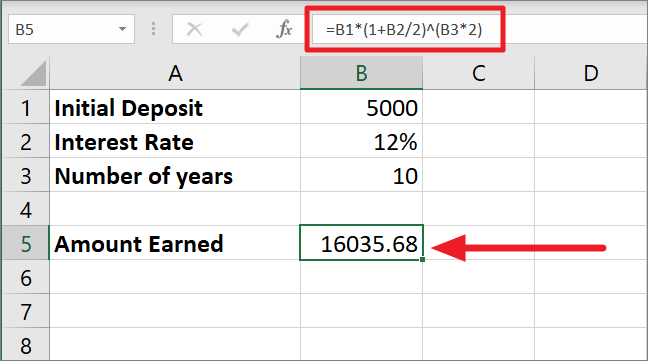
ご覧の通り、半年複利の方が年複利よりも獲得金額が若干高くなっています。複利計算の回数が多いほど、将来の価値は高くなります。

数式を使った四半期複利計算

月次複利の場合、1年間に3ヶ月ごとに複利を適用するので、複利計算の回数は1年に4回になります。先ほどの計算式と同じように、ここでは複利計算の回数が4回になるだけです。 ここでは、四半期ごとの複利計算の計算式をご紹介します。

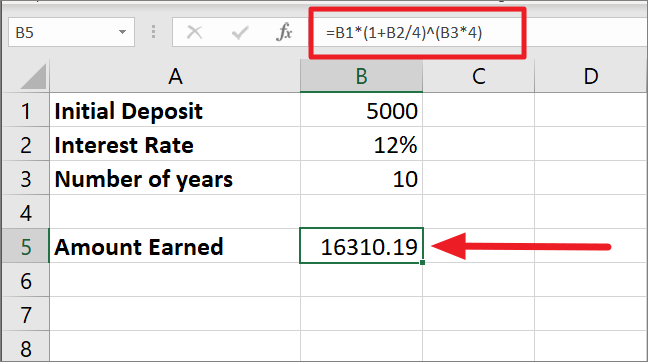
=b1*(1 b2/4)^(b3*4)

この式では、金利12％を4で割って、その結果の0.03を1に足すと、10が年数、4が1年間に複利計算する回数なので、40（10*4）乗の1.03になります。1.03を基数、40を指数とすると、3.27となる。最後に、3.27と最初の金額5000を掛けると、最終的な金額は16310.19となります。

月次複利計算の計算式

さて、次に月次複利計算について説明します。半年複利の場合、1年のうち毎月複利計算を行いますので、当然ながら1年間に複利計算を行う回数は12回となります。

下の式では、N値（複利計算の回数）を変更するだけで、月複利計算ができます。

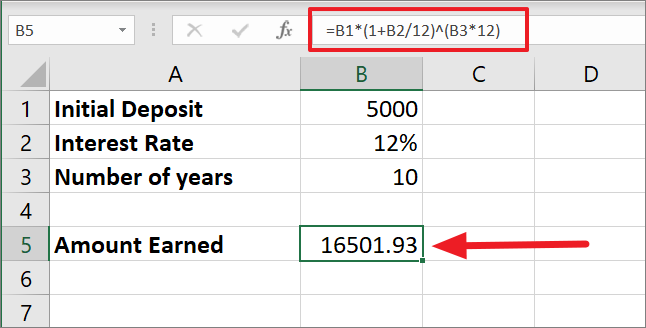
=b1*(1 b2/12)^(b3*12)

利息は1年のうち毎月複利で支払われるので、12％の金利を12で割ると0.01となります。0.01に1を足すと1.01となる。

1.01の120乗（10*12）は、10年間に複利計算される利息の総回数である。これで、3.300387になります。最後に、5000に3.300387を掛けると、最終的な残高は16501.93となります。

数式を使った週次複利計算

初期投資額に対する週次複利計算を求める場合、このセクションの数式を使用することができます。投資額に対する週次複利を計算する場合、1年間に複利計算される回数は52回になります。

週次複利計算の計算式はこちら、下の計算式をエクセルで実行してください。

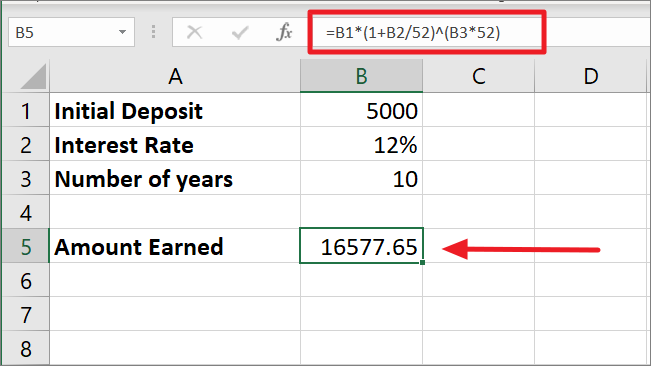
=b1*(1 b2/52)^(b3*52)

利息は1年のうち毎月複利で支払われるので、12%の金利を52で割ると0.002308となります。0.002308に1を足すと1.002308となります。

1.002308は520（10*52）乗となり、520は10年間に複利計算される総回数となる。利率と期間数を掛け合わせると、3.316059となります。最後に、5000に3.316059をかけると、最終的な金額は16577.65となります。

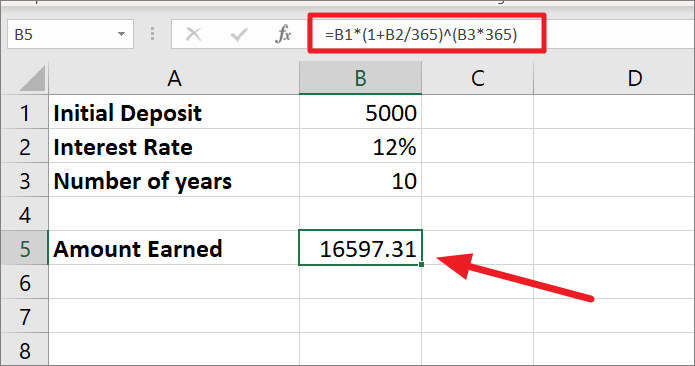
日次複利計算と計算式

日次複利は、投資や預金に対して、他の複利よりも高いリターンを得ることができます。日次複利方式では、前日の利息が加算された後、その日の利息が投資額に対して加算されます。

日割りの場合、1年のうち毎日複利計算を行うので、複利計算の回数は1年で365回となります。以下は、エクセルでの日割複利の計算式です。

=b1*(1 b2/365)^(b3*365)

日割り計算の場合、1年365日複利計算を行うので、金利を365で割る。そして、割った値に調整後の金利1を足すと、1.032877となる。

ここで、1.000328767を10*365（年数、複利計算の期間数）乗すると、3.31946071となります。最後に、3.31946071に5000ドルを掛けると、最終的な金額は16597.31ドルになります。

エクセルでの複利計算式テンプレート

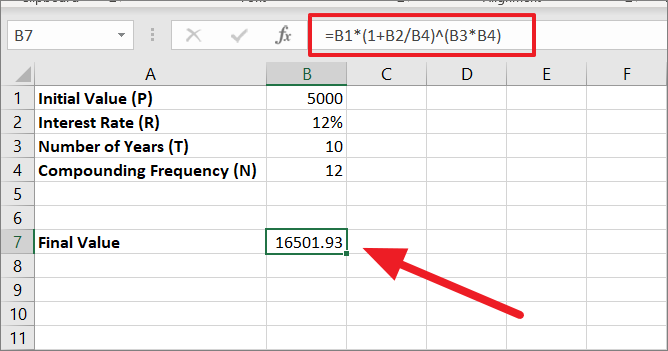
複利計算期間ごとに異なる計算式を作成する代わりに、複利計算期間が何であっても複利計算ができるオールインワンのエクセルテンプレートを作成することができます。ここでは、異なる複利計算期間に対して計算された複利をご紹介します。

=b1*(1 b2/b4)^(b3*b4)

上記の式は、これまでの式とそれほど変わりませんが、唯一違うのは、B4をN引数（複利計算の発生回数）として参照したことです。数式にN引数を手入力する代わりに、セルB4の複利計算回数を変更（4、12、52など）するだけで、同じ数式で異なる期間の複利を計算することができます。

エクセルでFV関数を使った複利計算

先に述べたように、Excelには複利の計算式がありません。しかし、FV()関数のような関数を使って複利や最終的な価値を計算することは可能です。FV関数とは、Future関数の略で、一定の支払額と金利をもとに、投資の将来価値（初期投資の複利）を計算するために使用されます。数式と同様に、FV()関数を使用して、年複利、四半期複利、月複利、週複利、日複利の計算を行うことも可能です。

シンタックス

以下は、FV()関数の一般的な構文です。

=FV(rate, nper, pmt, [pv], [type])

引数は

rate – 各期間において、金額に適用される一定の金利です。

nper – 1年間に発生する複利計算期間の総数です。月単位、四半期単位、月単位、年単位などがあります。

pmt – 各期間における追加の支払い。支払額がない場合は、0を値として指定する。この値が省略された場合は、PV引数を指定します。

pv (オプション) – 投資または融資の現在価値を表します。負の数で表現する必要があります。省略された場合、デフォルトは0（ゼロ）です。

type（オプション） – 支払（EMI）が期間の開始時に行われるか、期間の終了時に行われるかを指定します。EMIが期間開始時に支払われる場合は0を、期間終了時に支払われる場合は1を入力してください。省略した場合は、0がデフォルトとなる。

さて、FV関数とその引数を理解したところで、いくつかの例で使ってみましょう。

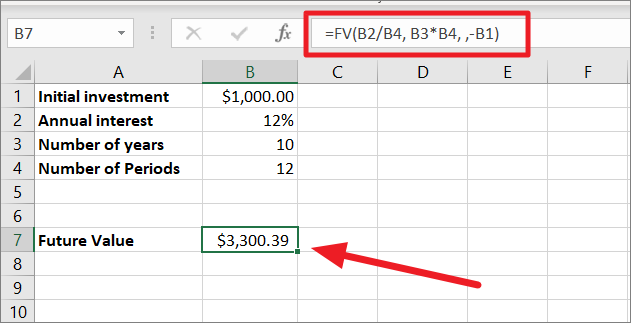
2000ドルを年利6%で5年間投資するとします。異なる複利計算期間での投資額の将来価値を計算してみましょう。

FV関数による月次複利計算

まず、追加支払のない月複利の投資について、その将来価値を計算してみましょう。以下は複利の計算式です。

=fv(b2/b4, b3*b4, ,-b1)

上の式で

  • 利率のパラメータはB2/B4すなわち12/12または0.012/12であり、これは12%の利率が毎月（12）回複利計算されるからです。
  • nperは、5年に複利計算の回数をかけたものです。
  • pmtは、追加の支払いをしないので、空白にしています。
  • 引数pmtを空白にしたため、引数pvを指定する必要があります。B1が初期値なので、これを引数PVと呼びます。流出なので負数で表します。

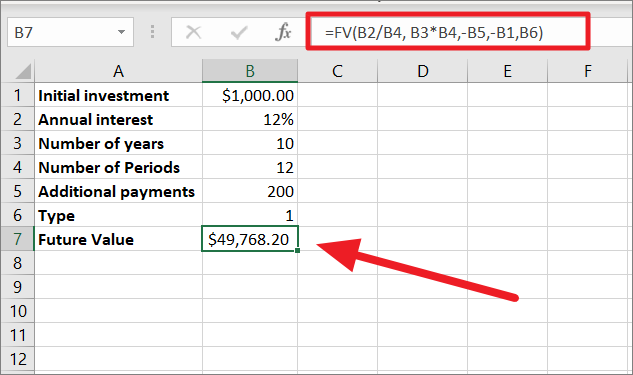
さて、FV複利の公式が追加支払いでどのように機能するかを見てみましょう。引数pmtを追加することで、上の式の容量を拡張することができます。

=fv(b2/b4, b3*b4,-b5,-b1,b6)

この式と前の式の違いは、「追加支払額」という引数が追加されていることだけです。現在価値に200を追加拠出するので、追加支払額を入力するか、その値の入ったセルを数式で参照する。追加払いを数式に追加する際、追加引数の種類も指定しておきます。複利計算期間の最初に追加支払いを行う場合は「1」を入力し、期間の最後に支払いを行う場合は「0」を入力します。

まず、以下のように表に必要な値を追加し、それに応じて計算式を調整します。ご覧のように、追加支払いで将来価値が大幅にアップします。

複利で得られる利息だけを得るには、最終的な価値から初期投資額を差し引けばよいのです。

=将来価値-初期価値=49,768 – 1000=48,768

初期値から10年間、毎月の複利計算で得られる利息は48,768円です。

ここで、日次、週次、月次、四半期、年次のすべての複利計算期間について、同じFV計算式を使用することができます。計算式は何も変更する必要はなく、表の「期間数」（複利計算の頻度）の値だけを変更すれば、結果は自動的に調整されるのです。

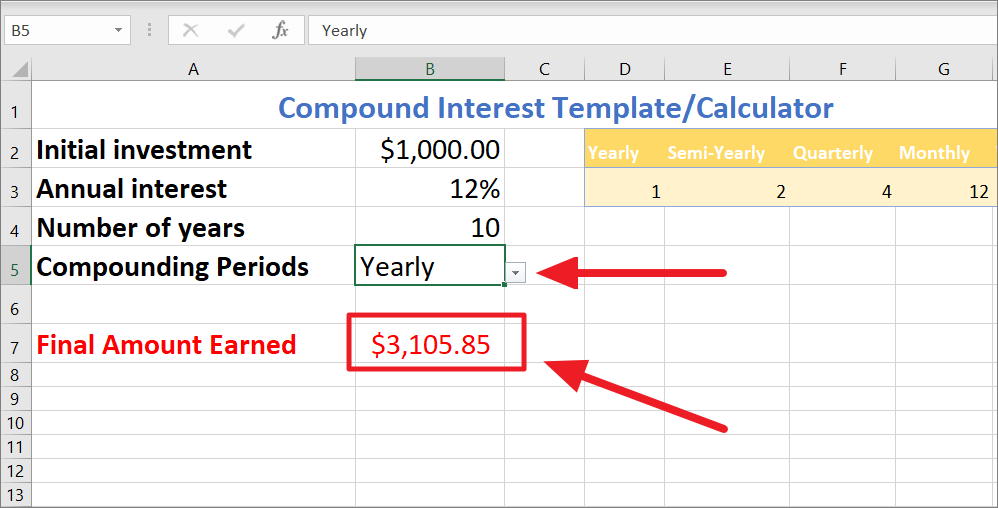上記のテンプレートは、こちらからダウンロードできます。

EFFECT関数で年内複利を計算する

エクセルのEFFECT関数は、名目金利から実効年利を計算します。EFFECTは、複利計算期間の異なる金融ローンを比較する際に便利です。年内複利とは、1年に1回より頻繁に複利計算される利息を意味します。

EFFECT関数のシンタックスです。

=EFFECT(nominal_rate, npery)

ここで

  • nominal_rate。名目金利を10進数で表したもの。
  • npery:1年間の複利計算の回数。

例えば、名目金利が5で四半期ごとの複利計算をした場合の年利を計算する場合は、以下の式を使用する。

=EFFECT(8%, 4)

0.0506となり、実効年利率は5.06となります。さて、上記のEFFECT関数を使って、実効的な複利の計算式を作ることができます。

EFFECT関数を使用して実効複利を計算するには、次の構文を使用します。

=p (p*effect(effect(r,n)*t,t))

ここで

P – 元本金額

R – 利息率

N – 1年間に複利計算が行われる回数（期間）

T – 年数

例

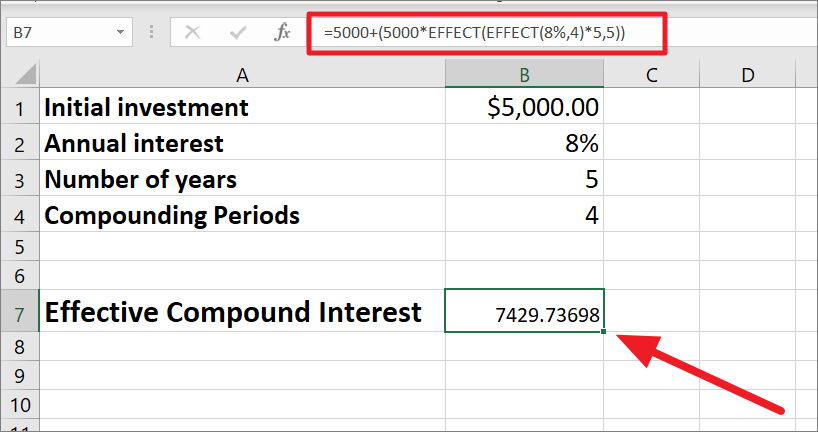
=5000 (5000*EFFECT(EFFECT(8%,4)*5,5))

ここでは、元本が5000ドルなのでP=1000、金利が8%なのでR=8%と入力します。四半期複利のため複利回数は4回、すなわちN=4です。Effect関数は4回繰り返され、そのうちの1回は年複利期間用にネストされ、さらに4倍されることで複利率を1年に分散させる。

FVSCHEDULE 関数を使って異なる金利で複利計算する

Microsoft ExcelのFVSCHEDULE関数は、一連の複利金利に基づく投資の将来価値を計算するためにも使用できます。FVSCHEDULE関数の計算式は以下の通りです。

FVSCHEDULE(プリンシパル、スケジュール)

ここで

  • プリンシパル：投資の初期金額
  • schedule: 投資の各期間における金利を表す、金利の配列または範囲。この配列は、任意の数の金利を含むことができます。

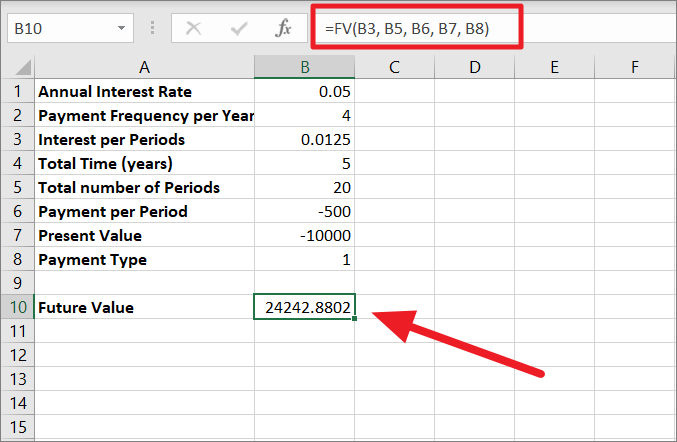
例1,000ドルの投資を行い、第1期は5%、第2期は6%、第3期は7%の金利がつくとします。さて、その投資の将来価値を計算してみましょう。

FVSCHEDULE関数を使って、投資の将来価値を計算する例を紹介します。

=fvschedule(b1, b2:b4)

ここで、B1は元本金額、B2:B4は金利の範囲である。

不定期積立金の複利計算を手動で行う場合

残念ながら、同じFVの計算式を使用して不定期預金の複利を計算することはできません。しかし、不定期預金の複利計算のための表を作成することができます。ここでは、不定期預金による複利計算のテーブルを作成する手順を説明します。

まず、下図のように期間（月番）、開始残高、入金額、終了残高の列を持つテーブルを作成します。そして、期間欄の下に期間をいくつでも追加することができます。これは3年分の四半期複利計算なので、合計12期間です。

四半期連続複利の将来価値

例えば、1000ドルを年利5or5年の継続複利で運用した場合、その期間後の将来額はどうなるでしょうか。四半期複利なので、年数を複利計算の期間数（4）で割ります。Excelでは「e」を数学的定数としてカウントしないので、EXP()関数を使って指数値を計算することにします。

=PV * Exp(r*t/n)

ここで

n – 1年間の複利計算期間の数。

例

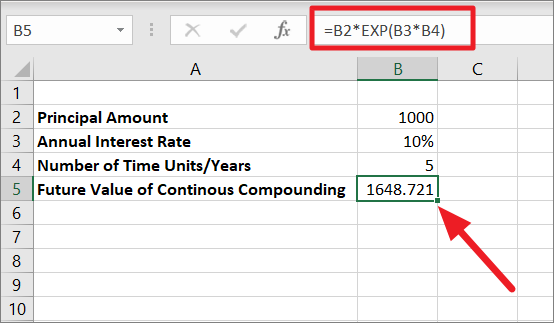
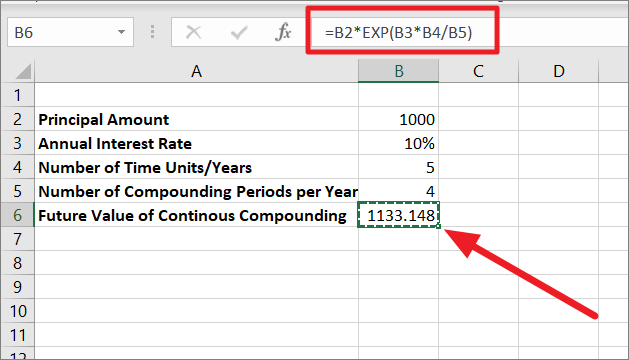
=B2*EXP(B3*B4/B5)

上式で、B2は元金（PV）、B3は利率（r）、B4は時間年数（n）、B5は1年当たりの複利計算の回数です。

時間単位を複利計算の期間数（10%/4=1.25）で割って、利率を掛けたものです。EXP 関数は、定数 e のべき乗の値 (0.125) を返します。その後PV(1000)に定数の値(1.133148)を掛けると、連続複利計算の金額は1133.148となります。

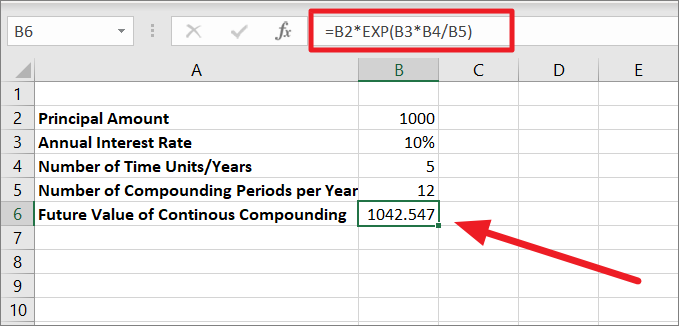
毎月の連続複利の場合の将来価値

同じ価値と利息について、毎月の複利で将来価値（FV）を計算したい場合は、以下の式を使用しますが、表中の複利の期間を変更してください。

=B2*EXP(B3*B4/B5)

上式で、B2は元金（PV）、B3は利率（r）、B4は時間年数（n）、B5は1年当たりの複利計算の回数です。

日次連続複利の将来価値

日次連続複利の計算式は同じですが、表中の複利計算の期間数を変えています。他の複利計算と異なり、連続複利運用の場合、複利計算期間が長くなるにつれて、将来価値が減少します。

=b2*exp(b3*b4/b5)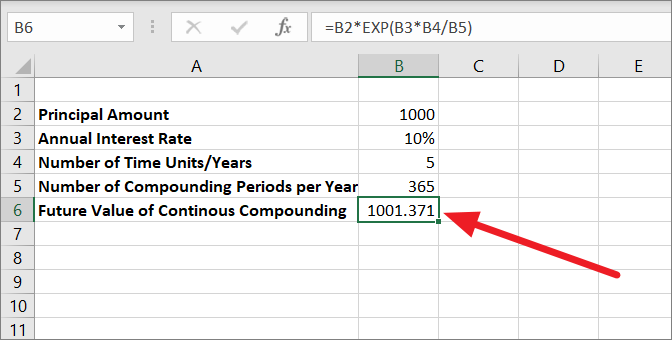

What-IF分析で複利を計算する

ExcelのWhat-If分析を使用して複利を計算することもできます。ExcelのWhat-If分析は、特定の結果に対する異なる入力値の影響を分析し評価するために使用されるツールです。これはデータテーブルを使用して行うことができ、複数の入力値をテストし、対応する結果をグリッド形式で確認することができます。

データテーブルは1次元または2次元のテーブルで、入力値はそれぞれ行または列のヘッダーで変更される。そして、入力値の組み合わせごとに、表の本文で計算式の結果を見ることができる。

1変数データ表で複利計算をする

Excelの1変数データ表は、1つの入力値の変化が計算式の結果にどのように影響するかを確認するためのツールです。1変数データテーブルは、金利または初期金額を変更し、それが最終的な金額にどのように影響するかを見ることによって、複利を計算するために使用することができます。以下は、Microsoft Excelでの例です。

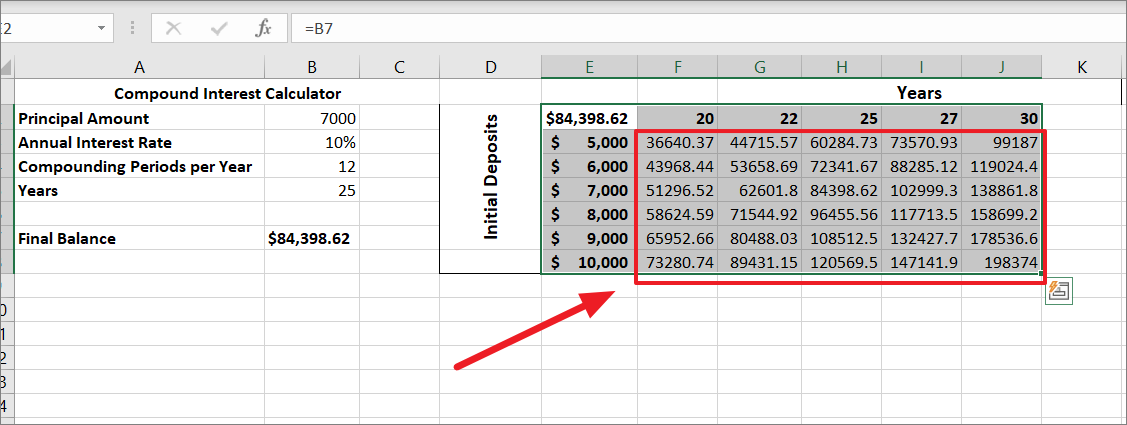
あなたは、毎月10オンスの金利を提供する銀行があることを知り、25年間で10万ドルを貯めたいと考えています。この目標を達成するために、最初の預金はいくらにすべきでしょうか？

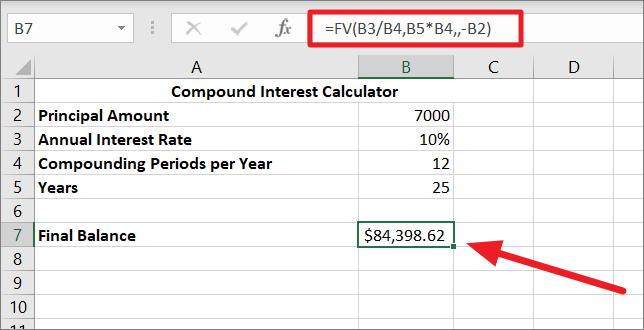
異なる値をテストするために、まず、FV関数を使って以下のような複利計算機を作りましょう。

=FV(B3/B4,B5*B4,,-B2)

下のスプレッドシートでは

  • B7 には、最終残高または将来の残高を計算するために使用される FV 式が含まれています。
  • B2 はテストしたい入力値（初期預金）です。

では、5000ドルから10000ドルまでの初期預金に基づいて、25年後の貯蓄額がどうなっているかを、1変数のデータ表を使ってWhat-If分析で確認してみましょう。

Excelで1変数のデータテーブルを作成するには、次の手順に従います。

変数値用のデータテーブルを作成し、1列または1行に渡って値を入力する必要があります。テーブルは、列指向または行指向のどちらでもかまいません。以下の例では、異なる入力値を列 (D4:D9) に入力し、その横に結果を表示するための空白の列を1つ残しています。

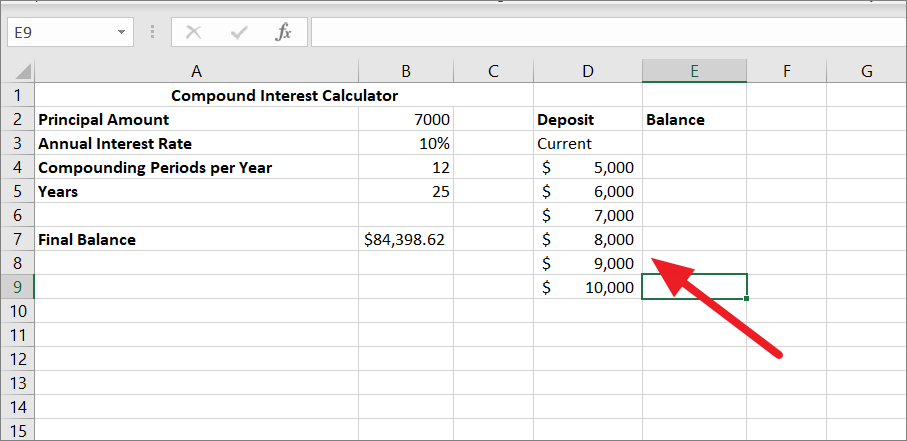
次に、この単純な数式 =B7 を変数値の 1 行上、1 セル右のセルに入力し、このセルと元のテーブルの数式セルをリンクさせます。この例では、それはセルE3です。こうすることで、将来的に数式を変更した場合でも、結果が自動的に更新されます。

ただし、E3に複利計算式を直接入力することも可能です。

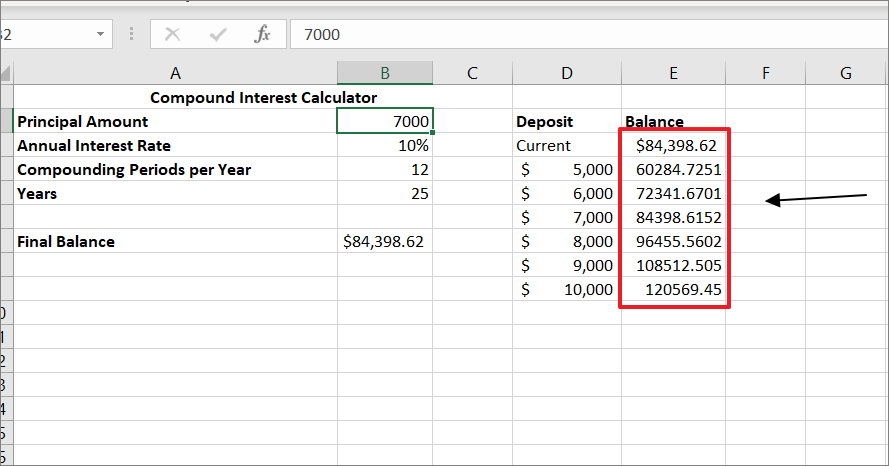
これで、異なる初期預金額と25年後の最終残高の1変数表が出来上がりました。そして、このデータ表を使って、投資に最適な預金額を決めることができるのです。

また、「預金」欄の変数を変更することで、さらに結果を検証することができます。

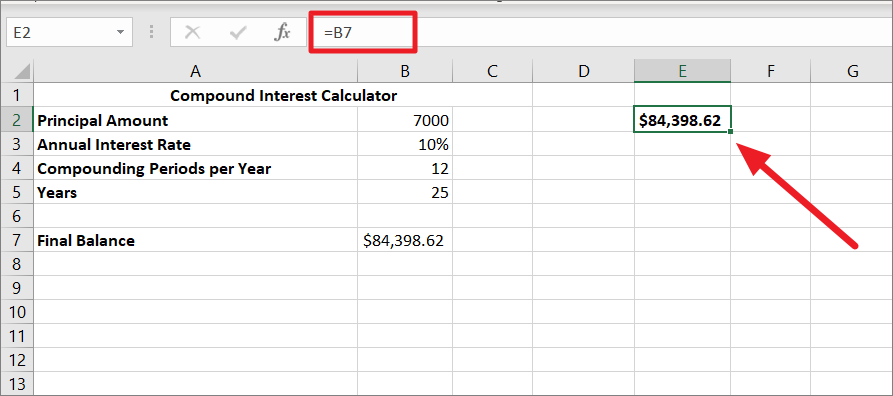
変数値や結果を収めるために、右側に十分な空の列、下に空の行があることを確認する。

次に、同じ列の数式（E2）のすぐ下に、1組の変数値（初期預金額または年数）を入力します。そして、もう一組の入力値を数式の右側、同じ行に入力します。この例では、初期預金額を E3:E9 に、年数を F2:J2 に入力しました。

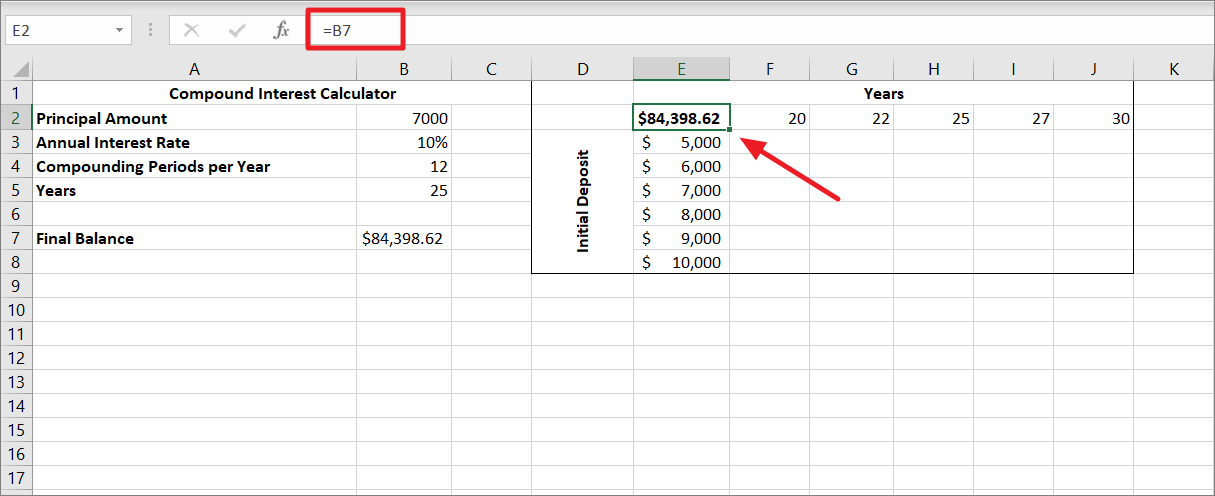
その後、数式を含むデータテーブルの範囲全体、入力値のセル、結果の空のセルを選択します。ここでは、範囲D1:J9を選択しました。

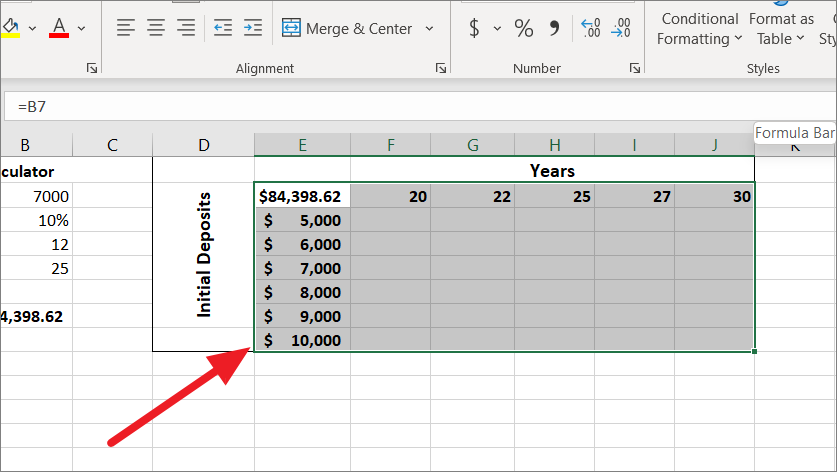
次に、「データ」タブに切り替え、「予測」グループの「What-If分析」ボタンをクリックし、メニューから「データテーブル…」を選択します。

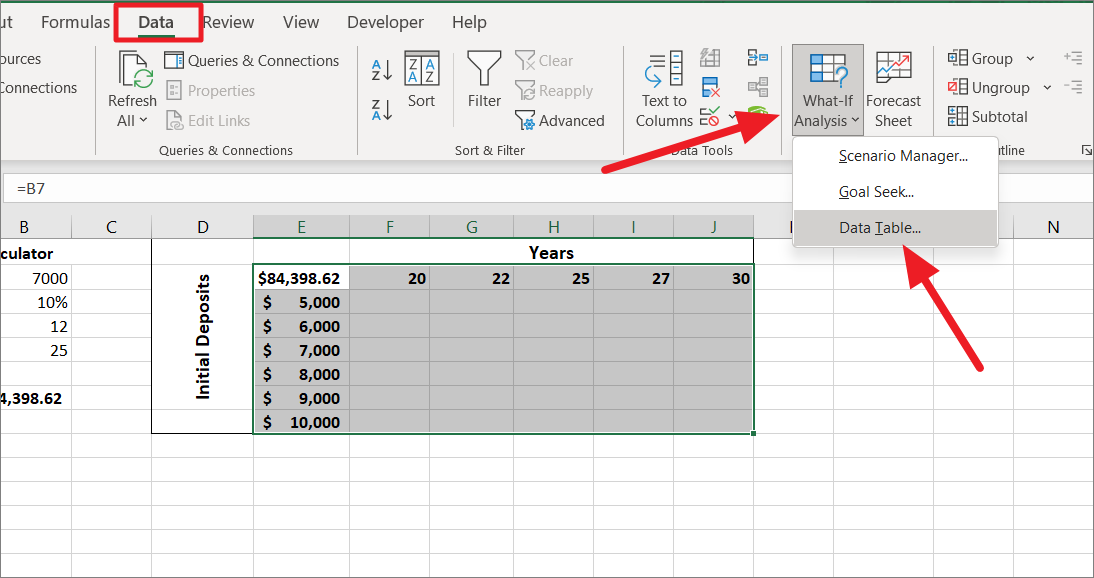
データテーブル」ダイアログボックスで、「行入力セル」フィールドをクリックし、「年」の値を含むセル(B5)を選択します。

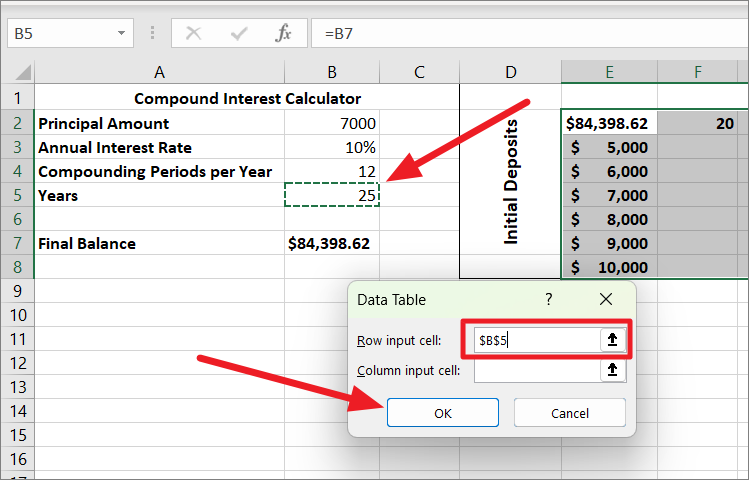
次に、「列入力セル」フィールドをクリックし、初期投資値のあるセル（B2）を選択し、「OK」をクリックします。

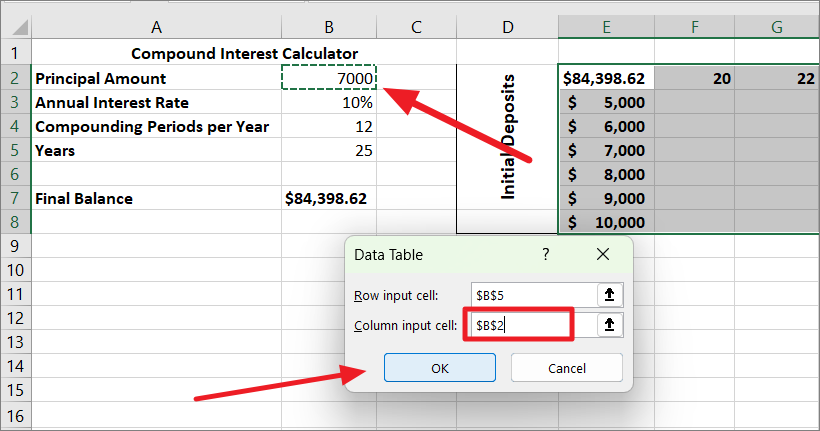
OK」をクリックすると、Excelはすぐにデータ・テーブルの結果のセルに入力します。これで、2つの異なる変数のセットがFV式の結果に与える影響を見ることができます。

エクセルで年平均成長率(CAGR)を計算する方法

これまで、いくつかの方法で複利の計算方法を学びました。今回はさらに一歩進んで、エクセルで年平均成長率（CAGR）を計算する方法を見ていきましょう。複利と年平均成長率 (CAGR) は、どちらも時間の経過に伴う成長を測定するために使用されるという点で関連しています。しかし、成長を測定する方法は異なります。

年間平均成長率（CAGR）は、投資が時間の経過とともに化合すると仮定し、指定された期間における投資の平均収益率を表す金融指標です。年などの特定期間における投資やポートフォリオの平均成長率を計算するために使用されます。

年間平均成長率（CAGR）は、ビジネス、財務計画、財務モデリング、および投資分析に非常に役立ちます。CAGRを計算するには、投資の開始値、終了値、期間（年）の数という3つの主要な入力が必要です。

CAGRの公式

CARG式の構文は以下の通り。

CAGR = (終了値/開始値)1/n – 1

ここで

  • Ending value – 投資期間終了時の残高を指します。
  • Beginning value – 投資期間開始時の投資残高。
  • n – 投資した年数.

エクセルで演算子を使用してCAGRを計算する

CAGRを計算する直接的な方法は、演算子を使用することです。CAGRを計算するには、上記の一般的な数式を使用します。

下のスプレッドシートに、ある会社の売上データがあるとします。

A列には、収益が得られた年度が書かれています。B列には、それぞれの年の会社の収益が書かれています。エクセルのCAGRの計算式で、収益の年間成長率を計算することができます。

直接法でCAGRを計算する場合は、以下の計算式を入力してください。

=(B11/B2)^(1/9)-1

下の例では、投資の開始値はセル B2 に、終了値はセル B11 にある。投資期間の開始から終了までの年数（期間）は9年です。通常、各投資サイクル期間は1年始まり、翌年に終了するため、この例の場合、最初のサイクルの期間は2011-2012年、最後のサイクルは2019-2020年です。つまり、投資年数の合計は「9」です。

結果は、上記のようにパーセンテージではなく、小数で表示されます。パーセンテージに変換するには、「ホーム」タブで、「数値」グループの「一般」というドロップダウンをクリックし、「% パーセンテージ」オプションを選択します。

さて、セルB13には「11.25%」という年複利成長率が表示されました。これは、全期間における単一の平滑化された成長率です。

Excel で POWER 関数を使用して CAGR を計算する

Excelで年複利成長率（CAGR）を計算するもう一つの簡単な方法は、POWER関数を使用することです。POWER関数は、CAGR関数の^演算子を置き換えるものです。

POWER関数の構文です。

=POWER(数値,べき乗)

POWER関数の引数。

  • number – 終了値（EV）を開始値（BV）で割ることによって得られる基数です（EV/BV）。
  • power – 結果を期間で割った指数（1/期間数(n)）に上げることである。

さて、このように引数を定義して、CAGR値を求めます。

=POWER(EV/BV,1/n)-1

この式を例題に適用してみよう。

=POWER(C11/C2,1/A11)-1

その結果

Excel で RATE 関数を使用して CAGR を計算する

RATE 関数は、Excel で CAGR を求めるために使用できる別の関数です。RATE関数の構文を見ると、6つの引数があり少し複雑に見えますが、一度関数を理解すると、CAGR値を求めるのにこの方法を好むようになるかもしれません。

RATE関数のシンタックスです。

=RATE(nper,pmt,pv,[fv],[type],[guess])

ここで

  • nper – 支払期間（ローン期間）の総数です。
  • Pmt (オプション) – 各期間での支払額です。
  • pv – これは、ローン/投資の現在価値を指定します（開始値（BV））。
  • [fv] – これは、ローン/投資の将来の価値、最後の支払い時（終了値（EV））を指定します。
  • [type] – これは、ローン/投資の支払期限を指定し、それは0または1のいずれかです。引数0は、支払いが期間の開始時に行われることを意味し、1は、支払いが期間の終了時に行われることを意味します (デフォルトは0です)。
  • [推測] – あなたが推測する利率です。省略した場合、デフォルトは10%です。

RATE関数に6つの引数があるのは、他の多くの財務計算に使用できるからです。しかし、第1引数（nper）、第3引数（pv）、第4引数（fv）の3つだけで、RATE関数をCAGR式に変換することができるのです。

=RATE(nper,,-BV,EV)

定期的な支払い（毎月、四半期、毎年）はしないので、第2引数は空欄にします。

RATE関数を使って年複利成長率を計算するには、次の式を使用します。

=rate(a11,,-c2,c11)

期間数を手動で計算したくない場合は、RATE式の第1引数にROW関数を使用します。これは、あなたのためにnprを計算します。

=rate(row(a11)-row(a2),,-c2,c11)

Excelで複利計算をするために必要なことは、これですべてです。このガイドがお役に立つことを願っています。

関連記事

Scroll to Top